MapPoEng -- main

MapPoEng = Mapping of Potential Energy
Mapování Potenciální Energie
říjen 2015, Petr Frantík
poslední aktualizace: únor 2017
http://mappoeng.kitnarf.cz

MapPoEng dokumentace (verze 1.23 a pozdější)
Petr Frantík

Obsah

Aktualizace
Úvod
Pojmy
Spuštění aplikace
Definice úlohy
Řízení výpočtu
Výstupy
Poznámky
Literatura

Aktualizace

v1.23 (20170216): Změna XML indexování u prvku Label. Čísluje se nyní o nuly (dříve od jedničky).
v1.21 (20170113): Přidán nový automatický mapovací nástroj DiagonalBaseComb.
v1.20 (20170110): Přidány nové automatické mapovací nástroje založené na obnovení stavu systému (CombX, CombY, DiagonalCombX a DiagonalCombY).
v1.19 (20161215): Umožněn export vizualizace ve formě obrázků formátu PNG.
v1.18 (20161129): Přidány nové automatické mapovací nástroje DiagonalSnake a DiagonalSpiral.
v1.16 (20161024): Přidány nové automatické mapovací nástroje (SnakeY, SpiralX, SpiralY, LabyrinthX, LabyrinthY) a byl přejmenován původní mapovací nástroj Automatic na SnakeX. Upraven výstup pro tabulkové procesory.
v1.15 (20161011): Zavedeno pole mapovacích nástrojů. Do této verze byl povolen pouze jeden mapovací nástroj. Nástroj k uchycení bodu ztratil argument mapper.
v1.14 (20160826): Přidání rámové vazby.
v1.12 (20160817): Zavedení styčníků.
v1.10 (20160816): Automatický mapovací nástroj.
v1.09 (20160816): Definiční soubor a jeho načítání za účelem generování úlohy.
v1.07 (20160422): Rozšíření výstupních dat.
v1.06 (20160311): Do výstupu přidány reakce působící na zachycený bod.
v1.05 (20150901): Výstup z aplikace ve formě stavového souboru.
v1.04 (20150828): Generování von Misesova nosníku z parametrů příkazového řádku.
v1.00 (20150625): První verze aplikace.

Úvod

Aplikace MapPoEng slouží k vytváření projekcí funkcí potenciální energie mechanických systémů do dvourozměrných map, viz obr. 1. Tyto mapy odhalují vlastnosti rovnovážných statických stavů systémů, slouží pro analýzu jejich stability a hledání bifukačních bodů.

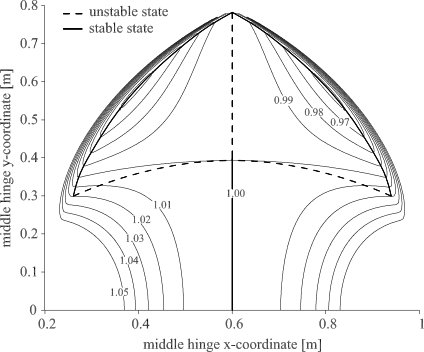
Obr. 1: Příklad výsledné mapy potenciální energie (symetrického von Misesova nosníku) vypočtené pomocí aplikace MapPoEng.

Pojmy

Potenciální energie: je energie mechanického systému daná jeho polohou v silovém poli a polohou jeho částí vůči sobě. Zde se jedná především o energii, kterou systém obsahuje díky svému uspořádání, více viz např. [1]. V případě pružné konstrukce se potenciální energie shromažďuje v její slačitelné hmotě.
Řízené posunutí: je způsob jak měnit tvar mechanického systému. Určitý bod, resp. body, systému jsou zachyceny a je jim udělováno posunutí dle požadavků uživatele. Pomocí řízeného posunutí se provádí mapování závislosti potenciální energie systému na poloze zachyceného bodu.
Bifurkační bod: je místo kde dochází ke kvalitativní změně stavu systému. Na obr. 1 jsou vidět čtyři bifurkační body v místech křížení tučných čar, které odpovídající stabilním a nestabilním rovnovážným statickým stavům.
Statický rovnovážný stav: je stav, při kterém je systém v klidu a v rovnováze. Do stabilního statického rovnovážného stavu se systém po malém vzruchu vrací, je zde lokální minimum potenciální energie. U nestabilního statického stavu způsobí vzruch jeho trvalé opuštění, systém má v jeho místě lokální maximum či sedlový bod.

Spuštění aplikace

Aby bylo možno aplikaci MapPoEng spustit, musí být v operačním systému nainstalována Java platforma (verze 1.8 a pozdější). Platformu lze stáhnout z adresy http://www.java.com/en/download/manual.jsp. Je-li Java platforma správně nainstalována, lze soubor aplikace mappoeng.jar spustit.

Aplikace MapPoEng se spouští buď přímo (kliknutím na soubor mappoeng.jar) nebo z konzoly operačního systému (pokud jí systém disponuje). Spuštění z konzoly je vhodné pro hromadné zpracování a pro sledování podrobných varovných či chybových výpisů. Spuštění z konzoly se provede zapsáním následujícího řetězce do konzoly operačního systému (v případě, že jsme přítomni v adresáři, kde je umístěn soubor mappoeng.jar):

java -jar mappoeng.jar

Definice úlohy

Aplikace MapPoEng analyzuje model určený v souboru definition.xml, jenž se musí nacházet v adresáři spolu se souborem aplikace. Soubor je typu XML, viz [2], díky kterému lze snadno číst a upravovat běžnými editory prostého textu, např. [3],[4],[5].

Soubor obsahuje data pro vytvoření modelu prutové konstrukce včetně způsobu její analýzy. Abstraktní struktura souboru je následující:

Kontejner
  Model
    Materiály
    Průřezy
    Styčníky
    Pruty
    Rámové vazby
  Mapování
    Nástroj k uchycení bodu
    Mapovací nástroje
  Nastavení pro dynamický výpočet
    Tlumení
    Numerická metoda

Kontejner (Container) je objekt, který sdružuje všechny ostatní objekty. Zajišťuje jejich vytvoření v pořadí, v jakém jsou uvedeny v souboru. Kontejner slouží rovněž jako databanka jejich referencí. Každý objekt v kontejneru má index, jehož hodnota odpovídá jeho pořadí v kontejneru, přičemž se počítá od nuly. Lze použít i záporné číslo, které značí index předcházející indexu aktuálního objektu. Aby bylo možno vytvořit stabilnější indexování, je k dispozici značkovací objekt Návěští (Label), díky kterému lze indexování vztáhnout relativně k indexu tohoto objektu, viz příklad dále.

Model je abstrakcí struktury složené ze styčníků a prutů, respektive z hmotných bodů a pružin. Styčníky je třeba definovat pro vzájemné spojení více prutů, umístění podpor a určení počátku a konce každého prutu.

Materiál (Material) definuje hodnoty fyzikálních parametrů hmoty konstrukce. Jedná se především o modul pružnosti a hustotu látky, kterou je konstrukce tvořena.

Průřez (Crosssection) stanovuje hodnoty geometrických parametrů průřezů prutů konstrukce. Jedná se především o plochu průřezu a tzv. druhý moment plochy (moment setrvačnosti průřezu).

Styčník (Joint) je bodem, kde začínají a končí pruty, kde dochází k jejich spojení a kam se umísťují podpory.

Prut (Beam) je abstrakcí tělesa s převládajícím jedním geometrickým rozměrem oproti zbývajícím dvěma. V aplikaci MapPoEng prut spojuje dva styčníky pružnou vazbou tvořenou hmotnými body a pružinami, tzv. FyDiK modelem prutu, viz [6].

Rámová vazba (FrameBind) vytváří ohybové provázání dvou prutů. Bez tohoto provázání se styčník dvou prutů chová jako kloub.

Mapování sdružuje definici metod a jejich parametrů sloužících pro analýzu chování modelu konstrukce.

Nástroj k uchycení bodu (PointRestrainer) slouží pro nalezení hmotného bodu, který bude pro účely analýzy uchycen (viz řízené posunutí).

Mapovací nástroje (Mappers) definují způsob a pořadí, jakým bude prováděna analýza modelu konstrukce, viz Řízení výpočtu.

Nastavení pro dynamický výpočet obsahuje další nastavení a metody pro provedení analýzy.

Tlumení (Damping) je součást dynamické simulace modelující tzv. útlum a sloužící pro ustálení systému do statického rovnovážného stavu.

Numerická metoda (NumericalMethod) umožňuje vybrat metodu výpočtu diferenciálních rovnic modelu pro jeho dynamickou simulaci.

Příklad obsahu definičního souboru

Následuje ukázka obsahu definičního souboru pro analýzu rámu tvořeného dvěma pruty spojenými v rámovém styčníku:

<Container package="cz.kitnarf.io.xml">
  
  <Steel package="cz.kitnarf.materials.steel" />
  
  <NumericCrosssection package="cz.kitnarf.crosssection" area="0.008457" secondAreaMoment="1.32e-5" />
  
  <Label package="cz.kitnarf.io.xml" name="POINTS" />
  <Joint package="cz.kitnarf.energymapping.io" x0="-5" y0="0" restraintX="true" restraintY="true" />
  <Joint package="cz.kitnarf.energymapping.io" x0="0" y0="5" restraintX="false" restraitY="false" />
  <Joint package="cz.kitnarf.energymapping.io" x0="5" y0="0" restraintX="true" restraintY="true" />
  
  <Label package="cz.kitnarf.io.xml" name="BEAMS" />
  <Beam package="cz.kitnarf.dynamicalsystem.space2d.macro" pointA="container[label[POINTS,0]]" pointB="container[label[POINTS,1]]" segmentCount="10" material="container[0]" crosssection="container[1]" />
  <Beam package="cz.kitnarf.dynamicalsystem.space2d.macro" pointA="container[label[POINTS,1]]" pointB="container[label[POINTS,2]]" segmentCount="10" material="container[0]" crosssection="container[1]" />
  
  <FrameBind package="cz.kitnarf.dynamicalsystem.space2d.macro" beamA="container[label[BEAMS,0]]" beamB="container[label[BEAMS,1]]" />
  
  <BeamPointRestrainer package="cz.kitnarf.energymapping.io" beam="container[label[BEAMS,1]]" pointIndex="0" />
  <KeyboardControl package="cz.kitnarf.energymapping" stepX="0.05" stepY="0.05" />
  <SnakeX package="cz.kitnarf.energymapping.mappers" simulationTime="5" stepX="0.05" stepY="-0.05" countX="200" countY="200" startOffsetX="-5" startOffsetY="0" />
  
  <ModelDamping package="cz.kitnarf.energymapping.io" size="1000"/>
  <SymplecticEulerMethod package="cz.kitnarf.dynamicalsystem" timeStep="0.0001"/>
</Container>

Řízení výpočtu

K dispozici jsou dva druhy metod ovládání výpočtu (Mapovací nástroje):

Řízení klávesnicí (KeyboardControl) akcemi uživatele, dovolující dosažení libovolné polohy uchyceného bodu a tím přesnější určení hledaných stavů a veličin, jako je poloha bifurkačního bodu, ověření existence daného stavu, a podobně.
Automatické (Automatic) prohledávání definované oblasti definovaným způsobem, sloužící pro získání velkého množství dat, umožňujících sestavení podrobné mapy.

Tyto mapovací nástroje je možno do definičního souboru uvést pod sebou vícekrát v libovolné variaci. Následující nástroje budou vyvolány ukončením běhu předchozího nástroje. Mapovací nástroj se ukončí buď automaticky nebo uzavřením okna nástroje uživatelem. Tato vlastnost aplikace MapPoEng umožňuje nejprve nalézt požadovaný stav konstrukce pomocí klávesnice, a poté spustit automatické mapování. Stav konstrukce dosažený v okamžiku ukončení zůstává při změně mapovacího nástroje zachován.

Řízení pomocí klávesnice

Plná funkčnost tohoto nástroje je spojena se zobrazením okna příkazového řádku, kam se vypisují aktuální údaje. Aplikaci je tedy vhodné spustit z tohoto okna, viz Spuštění aplikace. K dispozici jsou následující ovládací klávesy:

Šipky posunou uchycený bod o daný krok daným směrem (není-li bod uchycen bude posunutí dočasné).
Space vyvolá výpis aktuálních hodnot.
Backspace uvolní respektive upevní uchycený bod ve vodorovném směru.
S sníží krok na polovinu původní hodnoty.
W zvýší krok na dvojnásobek původní hodnoty.
U uloží aktuální stav do stavových souborů.

Automatické mapovací nástroje

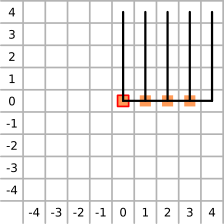
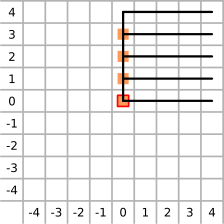
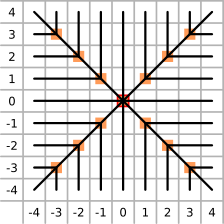
Tyto nástroje provádějí mapování potenciální energie v pravidelné mřížce rovnoběžné se souřadnými osami. Výpočet hodnot probíhá pomocí posunutí zachyceného bodu mezi sousedními body mřížky. Po každém posunutí zachyceného bodu se model ustaluje po dobu určenou parametrem čas simulace (simulationTime). Posunutí je prováděno různými postupy (viz také obrázek 2):

Had X (SnakeX) prohledávající mřížku po řádcích střídavě zleva doprava a zprava doleva.
Had Y (SnakeY) prohledávající mřížku po sloupcích střídavě zdola nahoru a zhora dolů.
Spirála X (SpiralX) prohledávající mřížku okolo počátečního bodu v rozšiřující se spirále s prvním posunutím ve směru osy X.
Spirála Y (SpiralY) dtto s prvním posunutím ve směru osy Y.
Labyrint X (LabyrinthX) prohledávající mřížku vodorovným i svislým směrem s prvním posunutím ve směru osy X.
Labyrint Y (LabyrinthY) dtto s prvním posunutím ve směru osy Y.
Diagonální had X (DiagonalSnakeX) diagonální had s prvním posunutím ve směru osy X.
Diagonální had Y (DiagonalSnakeY) dtto s prvním posunutím ve směru osy X.
Diagonální spirála X (DiagonalSpiralX) diagonální spirála s prvním posunutím ve směru osy X.
Diagonální spirála Y (DiagonalSpiralY) dtto s prvním posunutím ve směru osy X.
Hřeben X (CombX) prohledávání počínající ze základny ve směru osy X jdoucí ve směru osy Y. Po dosažení konce ve směru osy Y je obnoven stav na základně.
Hřeben Y (CombY) analogicky v druhém směru.
Diagonální hřeben X (DiagonalCombX) prohledávání počínající ze základny ve směru osy X a jdoucí diagonálně na obě strany. Po dosažení konce ve směru osy X je obnoven stav na základně.
Diagonální hřeben Y (DiagonalCombY) analogicky v druhém směru.
Hřeben s diagonální základnou (DiagonalBaseComb) prohledávání počínající z diagonální základny a jdoucí střídavě ve směru osy X a Y pro všechny kvadranty. Po dosažení konce v daném směru je obdnoven stav na základně.

Doplňme, že počáteční bod každého automatického mapovacího nástroje může být změněn v případě potřeby dvěma způsoby: Lze použít předcházejícího mapovacího nástroje nebo stanovit parametry startOffsetX a startOffsetY. Tyto offsety způsobí přesunutí zachyceného bodu na určené místo (relativně k poslední pozici zachyceného bodu).

SnakeX	SnakeY	SpiralX	SpiralY


LabyrinthX	LabyrinthY	DiagonalSnakeX	DiagonalSnakeY


DiagonalSpiralX	DiagonalSpiralY	CombX	CombY


DiagonalCombX	DiagonalCombY	DiagonalBaseComb

Obr. 2: Zobrazení postupu mapovacích nástrojů (znázorněno ve spolupráci s Martinem Kalinou).

Výstupy

Aplikace MapPoEng produkuje výstup ve formě tabulek čísel s vypočtenými hodnotami energie a složek reakce bodu upevnění, viz tabulka 1 vypočtená z definičního souboru definition.xml (výstupní soubor spreadsheet_energy.txt).

Každý automatický mapomací nástroj může být v definičním XML souboru rovněž doplněn atributem saveImage=true, který zajistí ukládání každého kroku vizualizace do obrázku typu PNG dle nastavení okna aplikace. Před započetím mapování má uživatel 10 sekund na nastavení okna.

Pro zobrazovnání rozsáhlých výsledných tabulek lze s výhodou použít aplikaci FuVis, viz [7].

y\x	0	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45
5.45	null	null	null	null	null	null	null	null	null	1.02E+08
5.4	null	null	null	null	null	null	null	null	8.05E+07	9.08E+07
5.35	null	null	null	null	null	null	null	6.16E+07	7.07E+07	8.06E+07
5.3	null	null	null	null	null	null	4.53E+07	5.31E+07	6.18E+07	7.10E+07
5.25	null	null	null	null	null	3.14E+07	3.81E+07	4.54E+07	5.34E+07	6.22E+07
5.2	null	null	null	null	2.01E+07	2.55E+07	3.16E+07	3.84E+07	4.58E+07	5.39E+07
5.15	null	null	null	1.13E+07	1.55E+07	2.03E+07	2.58E+07	3.19E+07	3.88E+07	4.63E+07
5.1	null	null	5024215	7926038	1.15E+07	1.57E+07	2.06E+07	2.61E+07	3.24E+07	3.93E+07
5.05	null	1255936	2897982	5186393	8126915	1.17E+07	1.60E+07	2.09E+07	2.66E+07	3.29E+07
5	1.08E-18	378786.1	1401114	3070306	5395107	8384360	1.20E+07	1.64E+07	2.14E+07	2.72E+07
4.95	null	117745	519572.9	1584263	3293046	5651058	8702325	1.24E+07	1.69E+07	2.20E+07
4.9	null	null	225758.9	670947.2	1798592	3560033	5957237	9083801	1.29E+07	1.74E+07
4.85	null	null	null	345830.1	835673.1	2044945	3872164	6316707	9532065	1.35E+07
4.8	null	null	null	null	471356.8	1016557	2325520	4231971	6733011	1.01E+07
4.75	null	null	null	null	null	604508.9	1216882	2643375	4642813	7210274
4.7	null	null	null	null	null	null	748144.7	1440520	3002344	5108817
4.65	null	null	null	null	null	null	null	905893.3	1691984	3407001
4.6	null	null	null	null	null	null	null	null	1082206	1976452
4.55	null	null	null	null	null	null	null	null	null	1282367

Tab. 1: Výstup ve formě tabulky.

Poznámky

Vyvinuto v rámci projektu GAČR 14-17997S – Globální citlivostní analýza v nelineární stavební mechanice, podporovaného Grantovou agenturou České republiky. Domovská stránka aplikace MapPoEng je http://mappoeng.kitnarf.cz.

Literatura

[1] Wikipedia, the free encyclopedia: Potential energy, http://en.wikipedia.org

[2] Wikipedia, the free encyclopedia: XML, http://en.wikipedia.org

[3] Wikipedia, the free encyclopedia: Notepad, http://en.wikipedia.org

[4] Wikipedia, the free encyclopedia: Vim, http://en.wikipedia.org

[5] Wikipedia, the free encyclopedia: PSPad, http://en.wikipedia.org

[6] Frantík Petr: Diskrétní model FyDiK2D, Sborník mezinárodní konference Modelování v mechanice 2009, VŠB-TU Ostrava, Česká republika, květen 2009, 10 stran, ISBN 978-80-248-2016-3

[7] Frantík Petr: FuVis, aplikace pro vizualizaci funkcí dvou proměnných, http://fuvis.kitnarf.cz, 2015.

MapPoEng dokumentace (verze 1.23 a pozdější) Petr Frantík